Q-learning is a model-free reinforcement learning algorithm to learn a policy telling an agent what action to take under what circumstances. It does not require a model of the environment, and it can handle problems with stochastic transitions and rewards, without requiring adaptations.
For any finite Markov decision process (FMDP), Q-learning finds an optimal policy in the sense of maximizing the expected value of the total reward over any and all successive steps, starting from the current state.
Q-learning can identify an optimal action-selection policy for any given FMDP, given infinite exploration time and a partly-random policy. “Q” names the function that returns the reward used to provide the reinforcement and can be said to stand for the “quality” of an action taken in a given state.
Reinforcement learning involves an agent, a set of states S, and a set A of actions per state. By performing an action, in A, the agent transitions from state to state. Executing an action in a specific state provides the agent with a reward (a numerical score).
The goal of the agent is to maximize its total reward. It does this by adding the maximum reward attainable from future states to the reward for achieving its current state, effectively influencing the current action by the potential future reward.
This potential reward is a weighted sum of the expected values of the rewards of all future steps starting from the current state.
The weight for a step from a state Δ t steps into the future is calculated as γ^Δt, where γ (the discount factor) is a number between 0 and 1 and has the effect of valuing rewards received earlier higher than those received later (reflecting the value of a “good start”). γ may also be interpreted as the probability to succeed (or survive) at every step Δ t.
Before learning begins, Q is initialized to a possibly arbitrary fixed value (chosen by the programmer). Then, at each time t the agent selects an action at, observes a reward rt, enters a new state st+1 (that may depend on both the previous state st and the selected action), and Q is updated.
The core of the algorithm is a Bellman equation as a simple value iteration update, using the weighted average of the old value and the new information:

Above is the Bellman Equation. Where Rt+1 is the reward received when moving from the state st to the state st+1, and α is the learning rate.
An episode of the algorithm ends when state st+1 is a final or terminal state. However, Q-learning can also learn in non-episodic tasks. If the discount factor is lower than 1, the action values are finite even if the problem can contain infinite loops.
To implement Q-learning we are going to use the OpenAI gym library which has tons of Reinforcement Learning environments, where Robots/Agents have to reach some goal.
The gym is a toolkit for developing and comparing reinforcement learning algorithms. It supports teaching agents everything from walking to playing games like Pong or Pinball.
For this article, we are going to use CartPole-v0 environment.
A pole is attached by an un-actuated joint to a cart, which moves along a frictionless track. The system is controlled by applying a force of +1 or -1 to the cart. The pendulum starts upright, and the goal is to prevent it from falling over. A reward of +1 is provided for every timestep that the pole remains upright. The episode ends when the pole is more than 15 degrees from vertical, or the cart moves more than 2.4 units from the center.
CartPole-v0 defines “solving” as getting an average reward of 195.0 over 100 consecutive trials.
Training Robot Using Q-Learning in Python
Above is the starting code for the CartPole agent. We’ve just added the for loop that goes up to 1000 iterations, and in those iterations, it will either stop or find a solution (reach goal state). We did that in order not to lose time when executing the starting code.
When it is time to go take action in a state, Q-Learning either takes random decision or goes in the Q table and chooses the maximum reward resulting action.
That is called policy and it is calculated with the expression below.
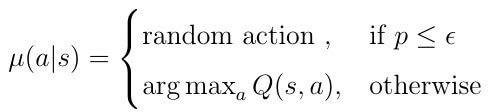
Epsiolon ϵ is a random generated number from a Uniform Distribution and it’s always between 0 and 1.
Next, we’ve modified the starting code so it stops when the mean of the sum of rewards is greater and equal to 195 and it is like that for the past 100 episodes.
From the code above, this is the output we’ve got:
Problem solved at 294th episode with average reward 294.0
So, the code above took 294 episodes to reach an average reward of 294. The first time it hit 195 was in the 195 episode.
Now we are going to implement the Q-learning algorithm to see if we can get this score earlier.
Above is the code we’ve implemented. It is much faster than what we’ve got with the starter code. Here is the output.
Problem solved at 26th episode with average reward 294.0
It finished in 26 episodes and the first time it hit 195 was in the 16th episode.
There were even faster solutions that used Deep Learning and some other techniques, but our idea was to make the model as simpler as possible. You can get great results if you use Deep Q-Learning or Double Q-Learning and those are topics that we are going to discuss in some of the next articles.
Conclusion
As you can see there are tons of powerful algorithms that can improve the speed of processing and the quality of your data. These days all of these algorithms are in the shadow of Deep Learning techniques.
Our advice is DO NOT use DEEP LEARNING everywhere, study the problem first and try with something simpler since that way you can understand the nature of the problem and the data.
Q-Learning or more precisely Deep Q-Learning is what OpenAI uses for its OpenAI Five algorithm that plays Dota2.
Open AI has tons of other interesting projects and environments that you can play with.
Projects like this took a lot of time since we are only 3 people in our team, so we would like to interact with you. If you have any suggestions for the next articles please let us know by messaging us in our private Facebook group or in the comments below.
We are also advocates for FREE education for everyone. If you like that idea check out our articles about:
- FREE Computer Science Curriculum From The Best Universities and Companies In The World
- How To Become a Certified Data Scientist at Harvard University for FREE
- How to Gain a Computer Science Education from MIT University for FREE
- Top 10 Best FREE Artificial Intelligence Courses from Harvard, MIT, and Stanford
- Top 10 Best Artificial Intelligence YouTube Channels in 2020
Like with every post we do, we encourage you to continue learning, trying, and creating.









